
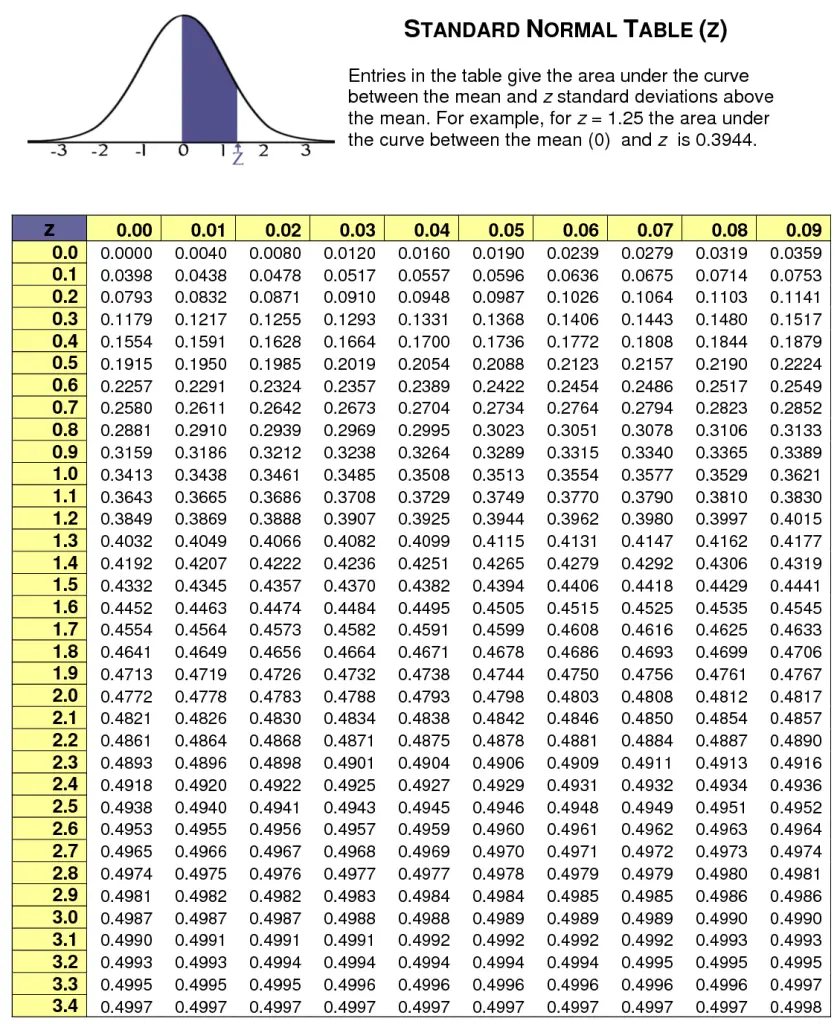
The shape and proportions of the bottom half are the same as the top half, which we already know. We use the symmetry around the midpoint of 0. Proportion below -ZĬolumn (3), the yellow proportion below -Z, is easier to work out. The answers are at the end of this article. Please calculate the proportion below a Z score of 1.60, missing letter (a) in table 2. This column is the green-shaded area in figure 2. So the green proportion below Z in table 2 column (2) above is calculated as 1 – 0.05 = 0.95 (95%). The blue proportion above Z from table 1 = 0.05 (5%). The reason for this is that the total population, by definition, adds up to a total proportion of 1 (100%). We calculate column (2), the green proportion below Z, as 1 (100%) less the proportion above Z (from table 1 above). The other information we can work out is in table 2 below. To do this, we use two of the important characteristics of the normal distribution: the total area under the curve is always 1 (100%) and the symmetry of the curve. Looking at figures 2, 3 and 4, we can now work out the green, yellow and pink proportions as well (even though these aren’t expressly set out in the ESA table). This is the blue-shaded area in figure 1. For example, for a Z score of 1.6449 (1.6449 standard deviations above the mean), 5% of the total modelled population is above this point. The proportions given in the table are the proportions of the total population, above the given Z score. In this case, it is a number of standard deviations above the mean. The ‘Z score’ in the table above is a number of standard deviations away from the mean. This is the version of the distribution that is set out in statistical tables like the one provided in your Economics and Statistical Analysis (ESA) exam, summarised below. The standard normal distribution has a mean of 0 and a standard deviation of 1. The standard normal distributionĪ standard normal distribution is a (standardised) transformed version of any normal distribution. The mean defines the midpoint of the normal distribution and the standard deviation defines how spread out it is.
STANDARD NORMAL TABLE 95 C TABLE HOW TO
Doug Williamson explains how to score full marks quickly and reliablyĪ normal distribution is an extremely useful (simplified) model for making predictions about real world distributions.
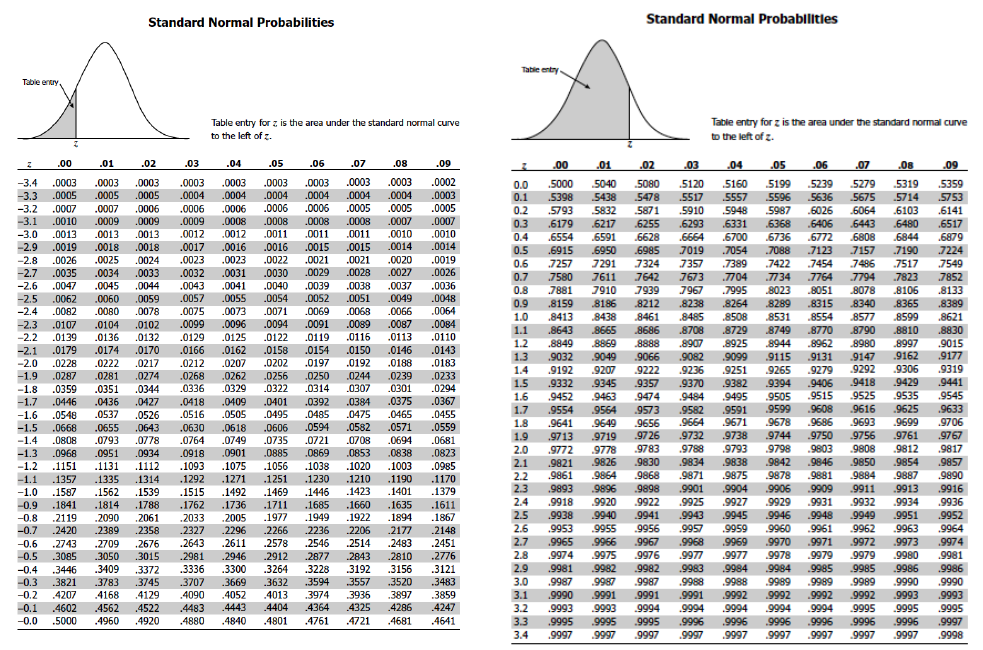
The z-table shows a z-score of approximately 1.28, for an area under the normal curve to the left of z (larger portion) of approximately 0.9.Normal distributions are often examined, and one particular mistake is commonly made. We need to find the z-score that corresponds to the area of 0.9 and then substitute it with the mean and standard deviation into our z-score formula. We know the mean, standard deviation, and area under the normal curve. The variable k is often called a critical value. Ninety percent of the test scores are the same or lower than k, and 10 percent are the same or higher. The 90 th percentile k separates the exam scores into those that are the same or lower than k and those that are the same or higher.
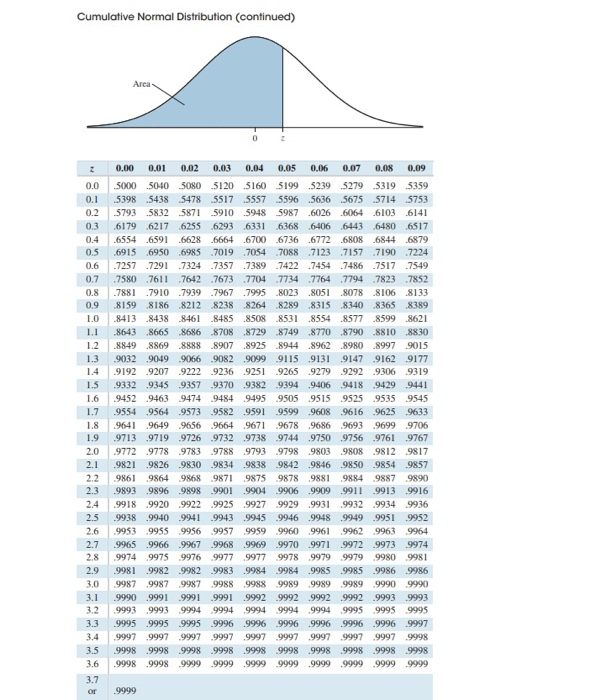
This time, we are looking for a score that corresponds to a given area under the curve. Shade the area that corresponds to the 90 th percentile. For each problem or part of a problem, draw a new graph.


 0 kommentar(er)
0 kommentar(er)
